Creating Isometric Games
Isometric games are games where the graphics emulate isometric projection. Because the camera orientation doesn’t change, the graphics are still technically 2D, but it’s common to refer to this as 2.5D to suggest that there’s some depth to the display.
Because we’re still working in two dimensions, we need to constantly account for this isometric viewpoint in all of our code and node configuration.
Everything here assumes that you are starting from zero knowledge, just as I did when I first started learning about this. The difference between tutorials on the subject and this page though is we’re starting with the required background knowledge in order to properly understand not only what we need to do, but why we’re doing it.
Background Theory
We consider the graphics to be isometric if the grid lines we use could have been created using a linear transformation. There’s more information below, but if your grid lines are still parallel to each other, you’ve done a linear transformation.
We’re going to be doing vector and matrix multiplication in order to work in this environment. Godot makes this pretty easy.
Common Ratios
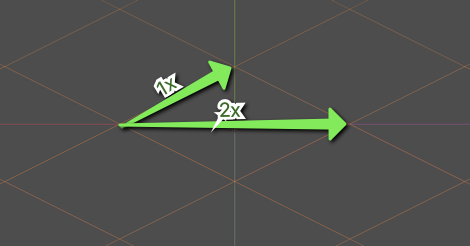
It’s common to use a 2:1 ratio on cartesian coordinates to achieve the isometric
look. This means that, to move on a grid, you move 2 pixels on the x
coordinate for every 1 pixel on the y coordinate.
This whole article will assume that we’re working with that 2:1 ratio.
If we held a standard 2D grid in our hands, what would we do to it to get to the isometric layout? We would take the grid, turn it 45 degrees, and then squish down on the new vertical axis. That’s fine, but how do we explain this to a computer?
We need to use linear transformations.
Linear Transformations
Brilliant.org provides a good definition of linear transformations on their wiki:
A linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector space.
For a nice primer on linear transformations, watch this video by 3Blue1Brown. Yes, it’s a video about math. No, you shouldn’t skip it. If you want to make video games, you need to know how this stuff works.